首页 百科文章正文

揭秘量子隧穿效应张朝阳的物理课中的方势垒隧穿概率计算

百科 2024年05月29日 02:22 1.2K+ 秉谦

量子隧穿效应是量子力学中一个非常神奇且基础的现象，它描述了粒子如何能够穿越经典物理学认为不可逾越的势垒。这一现象不仅在理论上具有重要意义，而且在实际应用中，如半导体器件、扫描隧道显微镜以及核反应等领域都有广泛的应用。本文将围绕量子隧穿效应，特别是通过方势垒的隧穿概率计算，来深入探讨这一量子世界的奇妙现象。

1. 量子隧穿效应的基本概念

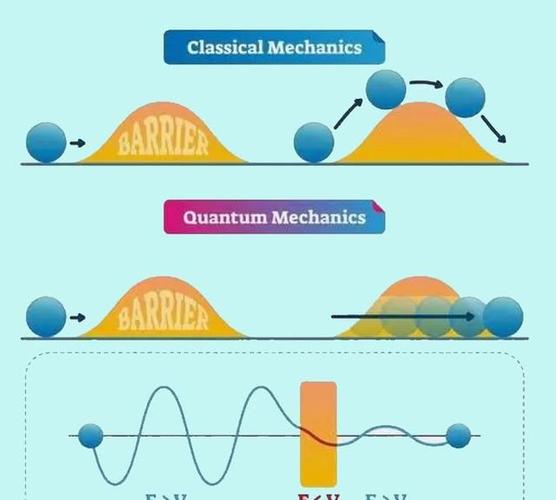
在经典物理学中，如果一个粒子的能量小于某个区域的势能，那么这个粒子就无法进入这个区域。然而，在量子力学中，情况并非如此。根据量子力学的波动理论，粒子可以被视为波，而波的传播并不受经典势垒的限制。因此，即使粒子的能量小于势垒的高度，它仍然有一定的概率穿透势垒，这种现象被称为量子隧穿效应。

2. 方势垒模型

为了计算隧穿概率，我们通常使用方势垒模型。在这个模型中，势能在一定区域内是常数，而在其他区域为零。具体来说，如果我们考虑一个一维情况，势能可以表示为：

$$

V(x) = \begin{cases}

V_0 & \text{if } 0 \leq x \leq a \\

0 & \text{otherwise}

\end{cases}

$$

其中，$V_0$ 是势垒的高度，$a$ 是势垒的宽度。

3. 隧穿概率的计算

在量子力学中，我们通过求解薛定谔方程来描述粒子的行为。对于方势垒问题，我们需要分别在势垒内部和外部求解薛定谔方程，并匹配边界条件。在势垒外部，粒子的波函数可以表示为入射波和反射波的叠加；在势垒内部，波函数则呈现出指数衰减的特性。

隧穿概率通常定义为透射波的强度与入射波的强度之比。通过求解薛定谔方程并应用边界条件，我们可以得到隧穿概率的表达式。在低能近似下，隧穿概率 $T$ 可以近似表示为：

$$

T \approx \frac{16E(V_0 E)}{V_0^2} e^{2\kappa a}

$$

其中，$E$ 是粒子的能量，$\kappa = \sqrt{2m(V_0 E)}/\hbar$，$m$ 是粒子的质量，$\hbar$ 是约化普朗克常数。

4. 张朝阳的物理课中的计算

在《张朝阳的物理课》中，他详细讲解了如何通过求解薛定谔方程来计算方势垒的隧穿概率。他首先介绍了量子隧穿的基本概念，然后逐步推导了隧穿概率的计算公式。通过具体的数值计算，张朝阳展示了不同能量和势垒宽度对隧穿概率的影响，使得这一复杂的量子现象变得直观易懂。

5. 量子隧穿效应的应用

量子隧穿效应不仅是理论物理学的一个重要研究对象，它在现代科技中也有着广泛的应用。例如，在半导体技术中，隧穿效应是场效应晶体管（FET）和隧道二极管等器件工作的基础。在扫描隧道显微镜（STM）中，隧穿电流的测量使得科学家能够观察到原子级别的表面结构。

6. 结论

量子隧穿效应是量子力学中一个非常基础且重要的现象，它揭示了量子世界与经典世界的根本差异。通过方势垒模型的隧穿概率计算，我们不仅能够更深入地理解这一现象，还能够将其应用于各种高科技领域。张朝阳的物理课通过详细的计算和解释，为我们提供了一个深入理解量子隧穿效应的窗口。

通过这篇文章，我们不仅回顾了量子隧穿效应的基本理论，还通过具体的计算实例加深了对这一现象的理解。量子隧穿效应不仅是理论物理学的一个重要研究领域，它在现代科技中的应用也展示了量子力学的巨大潜力。

标签： 蔡崇信cnbc采访视频 专访蔡崇信 蔡崇信500块追随马云 蔡崇信 加入阿里

相关文章

大金科技网  网站地图 免责声明：本网站部分内容由用户自行上传，若侵犯了您的权益，请联系我们处理，谢谢！联系QQ：2760375052 沪ICP备2023024866号-3