首页 百科文章正文

探索量子世界的基石二能级系统的能量本征态解析

百科 2024年05月29日 04:41 417 佳殷

在量子力学的奇妙世界中，二能级系统作为一个基础且重要的模型，广泛应用于量子计算、量子信息处理以及量子光学等领域。《张朝阳的物理课》深入浅出地介绍了这一主题，帮助我们理解如何求解二能级系统的能量本征态。本文将围绕这一主题，详细解析二能级系统的基本概念、数学描述以及求解能量本征态的方法。

1. 二能级系统的基本概念

二能级系统是指量子系统中只包含两个能级的系统。这两个能级可以对应于原子中的两个电子态，或者是一个量子比特的两个状态。在量子力学中，二能级系统可以用一个简单的哈密顿量来描述，其形式通常为：

\[ H = \begin{pmatrix} E_1 & V \\ V^* & E_2 \end{pmatrix} \]

其中，\( E_1 \) 和 \( E_2 \) 分别是两个能级的能量，\( V \) 是两个能级之间的耦合项。

2. 求解能量本征态的数学方法

为了求解二能级系统的能量本征态，我们需要解哈密顿量的本征值问题。这可以通过求解本征值方程 \( H \psi = E \psi \) 来实现，其中 \( \psi \) 是本征态，\( E \) 是对应的本征能量。

对于上述的二能级哈密顿量，本征值方程可以写为：

\[ \begin{pmatrix} E_1 E & V \\ V^* & E_2 E \end{pmatrix} \begin{pmatrix} \psi_1 \\ \psi_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \]

这是一个二阶线性方程组，可以通过求解行列式 \( \text{det}(H EI) = 0 \) 来找到本征能量 \( E \)。

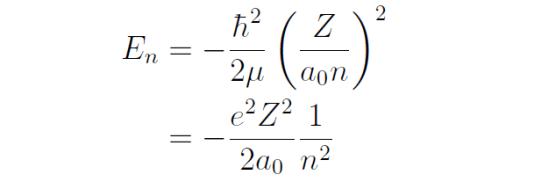
3. 本征能量的求解

展开行列式，我们得到一个关于 \( E \) 的二次方程：

\[ (E_1 E)(E_2 E) |V|^2 = 0 \]

解这个方程，我们可以得到两个本征能量：

\[ E_{\pm} = \frac{E_1 E_2}{2} \pm \sqrt{\left(\frac{E_1 E_2}{2}\right)^2 |V|^2} \]

这两个能量值对应于系统的两个本征态。

4. 本征态的求解

得到本征能量后，我们可以将这些值代入本征值方程，求解对应的本征态。例如，对于 \( E_ \)，我们有：

\[ \begin{pmatrix} E_1 E_ & V \\ V^* & E_2 E_ \end{pmatrix} \begin{pmatrix} \psi_1^ \\ \psi_2^ \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \]

解这个方程组，我们可以得到本征态 \( \psi_ \) 的表达式。同样，对于 \( E_ \)，我们可以求得本征态 \( \psi_ \)。

5. 物理意义与应用

二能级系统的能量本征态不仅具有理论上的重要性，还具有广泛的实际应用。例如，在量子计算中，量子比特通常被建模为二能级系统，其本征态对应于量子比特的两个基本状态。在量子光学中，二能级原子与光场的相互作用也是基于二能级系统的模型。

通过《张朝阳的物理课》的讲解，我们不仅学习了如何求解二能级系统的能量本征态，还理解了这一过程背后的物理意义和应用价值。这些知识为我们进一步探索量子世界提供了坚实的基础。

总结来说，二能级系统作为量子力学中的一个基本模型，其能量本征态的求解不仅揭示了量子系统的基本性质，也为量子技术的应用提供了理论支持。通过深入学习这一主题，我们能够更好地理解量子世界的复杂性和美妙。

相关文章

大金科技网  网站地图 免责声明：本网站部分内容由用户自行上传，若侵犯了您的权益，请联系我们处理，谢谢！联系QQ：2760375052 沪ICP备2023024866号-3