势场中的微观粒子演化薛定谔方程的解析之旅

经验 2024年05月31日 06:25 671 悦姗

在量子力学的世界里，微观粒子的行为与经典物理学中的粒子截然不同。它们不再遵循牛顿的运动定律，而是受到薛定谔方程的支配。《张朝阳的物理课》深入探讨了这一主题，特别是微观粒子在势场中的演化过程。本文将基于这一课程内容，详细解析薛定谔方程及其在描述微观粒子行为中的应用。

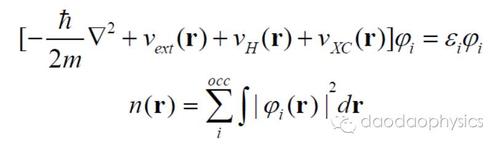
薛定谔方程是量子力学的核心方程，它描述了量子系统的状态随时间的变化，形式上可以表示为：

\[ i\hbar\frac{\partial \Psi(\mathbf{r},t)}{\partial t} = \hat{H}\Psi(\mathbf{r},t) \]

其中，\( \Psi(\mathbf{r},t) \) 是描述粒子状态的波函数，\( \hat{H} \) 是哈密顿算符，\( \hbar \) 是约化普朗克常数。哈密顿算符由动能算符和势能算符组成：

\[ \hat{H} = \frac{\hbar^2}{2m}\nabla^2 V(\mathbf{r}) \]

这里，\( m \) 是粒子的质量，\( V(\mathbf{r}) \) 是势能函数，描述了粒子在空间中受到的势场。

在势场中，微观粒子的行为受到势能函数 \( V(\mathbf{r}) \) 的影响。势场可以是吸引的，如原子核对电子的吸引，也可以是排斥的，如电子云之间的相互排斥。粒子的波函数 \( \Psi(\mathbf{r},t) \) 必须满足薛定谔方程，这决定了粒子在势场中的可能状态和演化路径。

求解薛定谔方程通常涉及分离变量法，将波函数分解为空间部分和时间部分。对于定态问题（即势能不随时间变化，\( V(\mathbf{r}) \) 是常数或仅依赖于空间坐标），波函数可以写成：

\[ \Psi(\mathbf{r},t) = \psi(\mathbf{r})e^{iEt/\hbar} \]

将此形式代入薛定谔方程，可以得到定态薛定谔方程：

\[ \frac{\hbar^2}{2m}\nabla^2\psi(\mathbf{r}) V(\mathbf{r})\psi(\mathbf{r}) = E\psi(\mathbf{r}) \]

这是一个本征值问题，\( E \) 是能量本征值，\( \psi(\mathbf{r}) \) 是相应的本征函数。

为了具体说明，我们可以考虑一个简单的模型——一维无限深势阱。在这个模型中，粒子被限制在 \( 0 < x < L \) 的区域内，势能在该区域外为无限大。这个问题的薛定谔方程可以解析求解，得到粒子的能量本征值和本征函数。

在势场中，微观粒子还表现出一种经典物理中不存在的效应——量子隧穿。即使粒子的能量低于势垒的高度，它也有一定的概率穿透势垒到达另一侧。这是量子力学中一个非常有趣且实用的现象，广泛应用于扫描隧道显微镜和半导体器件中。

通过《张朝阳的物理课》的深入讲解，我们不仅理解了薛定谔方程的基本形式和求解方法，还探讨了微观粒子在势场中的复杂行为。这些知识不仅加深了我们对量子世界的理解，也为未来的科学研究和工程应用提供了理论基础。

通过这篇文章，我们希望读者能够对微观粒子在势场中的演化有一个全面的认识，并对薛定谔方程的重要性有更深的理解。量子力学虽然抽象，但它揭示了自然界最基本的运作方式，是现代物理学不可或缺的一部分。

经典力学视角下的抗磁矩计算张朝阳物理课解析正常效应