首页 百科文章正文

柱坐标拉普拉斯算符是怎样的？《张朝阳的物理课》推导曲线坐标的算符

百科 2024年07月30日 08:32 530 琀欢

使用微分几何语言应该怎么求柱坐标下的拉普拉斯算符？电磁势的达朗贝尔方程是洛伦兹协变的吗？

7月28日12时，《张朝阳的物理课》第二百一十九期开播，搜狐创始人、董事局主席兼CEO、物理学博士张朝阳坐镇搜狐视频直播间，先在柱坐标下求出坐标基矢与单位基矢的关系，然后推导了柱坐标下的散度表达式，并借助柱坐标的度规、克氏符得到了拉普拉斯算符的具体表达式。介绍完微分几何在曲线坐标下的应用之后，张朝阳使用四维语言重新表述了电磁势的达朗贝尔方程，并指出其所隐含的协变性。

计算柱坐标系的度规与克氏符推导拉普拉斯算符的表达式

在上次物理直播课中，张朝阳介绍了球坐标下的度规、克氏符，以及相应的拉普拉斯算符的推导方法。这些方法也可以用在柱坐标系上，而且因为柱坐标系比球坐标要简单，因此所得结果也比球坐标的要简洁不少。

直角坐标使用的坐标分量为(x,y,z)，而在柱坐标使用的则是

其中柱坐标的z与直角坐标的z一样，而(r,ϕ)可以看作是x-y平面上的极坐标。

不管在什么坐标下，拉普拉斯算符的含义都可以看成是散度算符与梯度算符的复合：先作用完梯度算符后再作用散度算符。比如对于标量场f，它的梯度为

因为f是标量场，下指标的协变导数作用在其上就相当于普通偏导数作用在其上，因此有

如果总是考虑这些算符对标量函数的作用，那么可以直接将梯度算符看成是一个四维矢量，而无需再考虑其中的标量函数f：

上式的F虽然是一个算符，但是它也可以被看成是四维矢量，协变导数作用在其上遵循四维矢量的协变导数规则。读者如果不熟悉这种表示方式，可以自行在上式中补充上标量场f，这样将更容易理解。

为了求拉普拉斯算符的表达式，张朝阳把梯度算符F视为四维矢量并计算它的散度：

因此，整个推导的思路就可以归结为：先求梯度算符F的表达式，然后求克氏符，最后利用上式求出拉普拉斯算符的表达式。

如在上一次直播课中所指出的那样，坐标基矢与曲线坐标的单位基矢一般是不相同的。假设柱坐标的单位基矢为

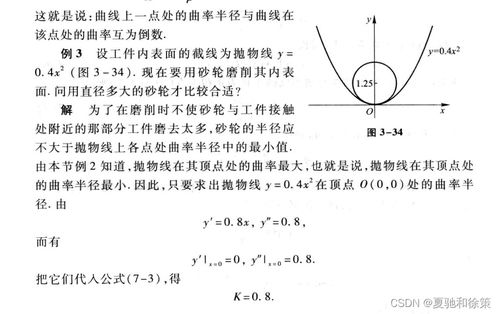
那么在柱坐标下位移微元可以按这组基下展开为

于是，得到了柱坐标系的坐标基矢为

另一方面，利用勾股定理可以得到

由此可以知道度规以及度规的逆分别为

感兴趣的读者也可以利用坐标基矢直接验证度规满足

接下来张朝阳开始计算梯度算符的表达式。在以前的直播课已经介绍过柱坐标的梯度算符为

现在它由单位基矢所表示，因此需要转换成坐标基矢的展开式才能得到相应的矢量分量，这很容易做到，结果为

因此F的各个分量分别为

这个结果也可以通过式(1)得到：

此结果与前面的结果是一致的。

利用这个结果，可以得到拉普拉斯算符为

为了得到最终的表达式，张朝阳计算了式中的克氏符，其中利用了度规矩阵的对角性质：

由于度规的各个分量至多只依赖于r，与其他坐标无关，因此只有当β=1时，上式才不为零。并且可以知道，在上式对α的求和中，只有α=2的项非零，柱坐标拉普拉斯算符是怎样的？《张朝阳的物理课》推导曲线坐标的算符因此有

于是，拉普拉斯算符可以被写为

此结果与以前的直播课所介绍的结果一致。

（张朝阳推导柱坐标下的拉普拉斯算符表达式）

使用四维语言表述电磁势的达朗贝尔方程

介绍完柱坐标的拉普拉斯算符推导方式之后，张朝阳转而介绍起麦克斯韦理论的四维形式。电动力学的相关知识在去年的物理直播课中已经介绍过了，但是当时没有采用四维形式进行讲解，因此电动力学的相对论协变性并不明显。根据当时的结果，洛伦茨规范条件下的电磁势所满足的方程为达朗贝尔方程：

考虑到μ₀*ε₀=1/c²，因此上式可以被写为

如果采用自然单位制，那么c=1，并使用坐标记号为

那么电磁势的达朗贝尔方程则可以被写为

注意到在四维平直时空上，度规为

因此有

这样就会得到

于是

通过构造

并且利用前面的结果即可将电磁势的达朗贝尔方程改写为

这就是四维形式下的达朗贝尔方程。由于这里的推导过程中使用了平直时空的度规及相应的协变导数，因此此结果只适用于平直时空的直角坐标。

可以证明，J是一个四维矢量，而∂ₐ∂ᵃ是一个标量算符，但是这还不足以证明上式的A是四维矢量。如果要想严格证明其为四维矢量，最直接的方法是求解该方程得到相应的解，然后利用这个解来证明相应的四维矢量性质，感兴趣的读者可以参考《张朝阳的物理课》第二卷。

（张朝阳介绍达朗贝尔方程的协变形式）

据了解，《张朝阳的物理课》于每周周日中午12时在搜狐视频直播，网友可以在搜狐视频APP“关注流”中搜索“张朝阳”，观看直播及往期完整视频回放；关注“张朝阳的物理课”账号，查看课程中的“知识点”短视频；此外，还可以在搜狐新闻APP的“搜狐科技”账号上，阅览每期物理课程的详细文章。

标签： 柱坐标拉普拉斯算符是怎样的？张朝阳的物理课推导曲线坐标的算符

相关文章

大金科技网  网站地图 免责声明：本网站部分内容由用户自行上传，若侵犯了您的权益，请联系我们处理，谢谢！联系QQ：2760375052 沪ICP备2023024866号-3